Hello, world! I have a clever problem for you. This is a problem from a Stanford course I took a couple years ago. It is simple yet brilliant, in my opinion. Here it is:

Suppose that you have a 3” × 3” × 3” cube of cheese subdivided into twenty-seven 1” × 1” × 1” smaller cubes of cheese. A mouse wants to eat the entire cube of cheese and does so as follows: she first picks any small cube to eat first, then moves to an adjacent small cube of cheese (i.e. a cube that shared a face with the cube that was just eaten) to eat next, then repeats this process. Is it possible for the mouse to eat the center cube of cheese last? If so, show how. If not, prove it’s impossible. (This problem is adapted from Problem 4E of A Course in Combinatorics, Second Edition by Lint and Wilson.)

We have two challenges here. The first is to decide whether we believe that the center cube can be eaten last. The second is to then prove our decision. When I first saw this problem, I first sketched a cube and tried to find a path that would allow me to reach all the cubes and end on the center cube. As it turns out, I spent a long time trying to find a way to do this because it isn’t actually possible to eat the center cube last. We can show why with an approach that involves basic arithmetic. We’ll prove the following theorem:

If a mouse picks any small cube to eat first and then moves to an adjacent small cube of cheese to eat next, then repeats this process, it is not possible to eat the center piece last.

Proof

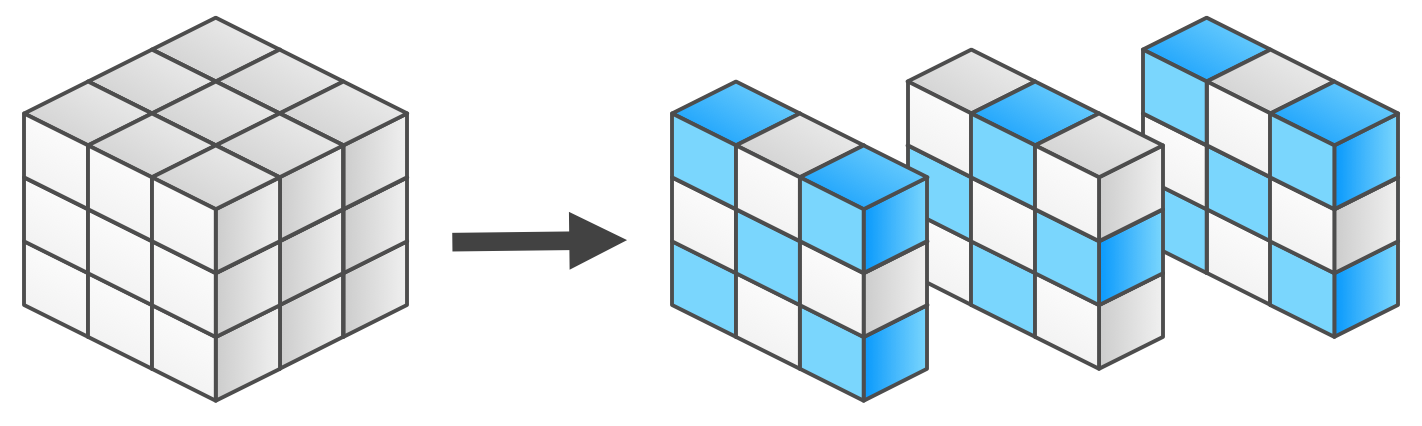
Imagine the cube of cheese is a Rubix’s cube, which has 27 blocks. These will represent our 27 small cubes of cheese. If we think of the cube of cheese as a 3D checkerboard, each of the 27 pieces of cheese can be placed into one of two groups that result in each piece being next to a piece of alternating color. If we have alternating blue and white pieces of cheese, we can group them as follows, as shown in figure 2 below:

The cube can be checkered into small blue and white cubes. There are 14 blue cubes and 13 white cubes, 27 cubes in total.

With this grouping, it is easier to see that the mouse can only move to adjacent pieces of cheese as defined by the problem: she can only move from a white piece to a blue piece and from a blue piece to a white piece as she eats her way through the cube.

Without loss of generality, let’s make the corner pieces of the cube blue and alternate the color of the smaller cubes for the rest of the cube as shown in the figure. With this grouping, the center piece of cheese is in the white group. This means that no matter which outer piece of cheese the mouse eats first, there is no way to eat the center piece of cheese last because there is one less piece of cheese in the white group than there are pieces of cheese in the blue group (there are 14 blue cubes and 13 white ones). To show this, let’s consider the two possible ways the mouse can start eating cheese:

Case 1: The mouse starts on a white piece, so her next piece must be a blue piece since she must always move to an adjacent and thus different color cube of cheese. Since the number of white pieces is one fewer than the number of blue pieces, if the mouse keeps eating pieces by alternating colors, she will run out of white pieces first and have one blue piece left. Since we know the center piece is white, the mouse will always eat the center piece before getting to the last blue piece. Thus, the center piece cannot be eaten last.

Case 2: The mouse starts on a blue piece, so her next piece must be white. Since there is one more blue piece than there are white pieces, the mouse will have to eat a blue piece last in this scenario as well since she’ll finish eating the white pieces first. Since we know the center piece is a white piece, the center piece cannot be eaten last in this case either.

We see that no matter which piece the mouse eats first, it is not possible to eat the center piece of cheese last. ■